C’est pas de la tarte !
Formulation du problème
Lorsque l’on mange pizza entre amis, nous apprécions goûter un petit morceau de la pizza de chacun. C’est pourquoi j’ai l’habitude sur ma part de pizza de rayon \(r=OB\) de 16 cm, de découper parallèlement à \([OB]\) une “bande” d’épaisseur \(e<r\) de 3 cm. Après avoir donné cette partie à un ami, il me reste donc une sorte de nouveau secteur angulaire \(MAC\). J’ai mesuré la différence de longueur entre les côtés \(MC\) et \(MA\) : \(d=MC-MA\) qui est de 2 cm.
Question : quel est l’angle \(\alpha=AOB\) de la part initiale ?
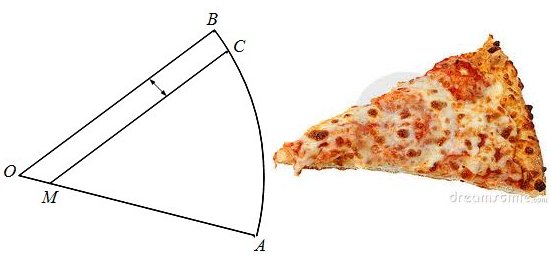
Solution
Les résultats qui vont suivre peuvent être vérifier “à la main” avec la simulation geogebra ci-dessous :
Télécharger la simulation geogebra
On cherche dans un premier temps à exprimer la différence de longueur \(\color{orange}{d=MC-MA}\) quand l’angle \(\color{green}{\alpha=AOB}\) varie, avec \(r\) et \(e\) fixés.
1. Calcul de la longueur MA
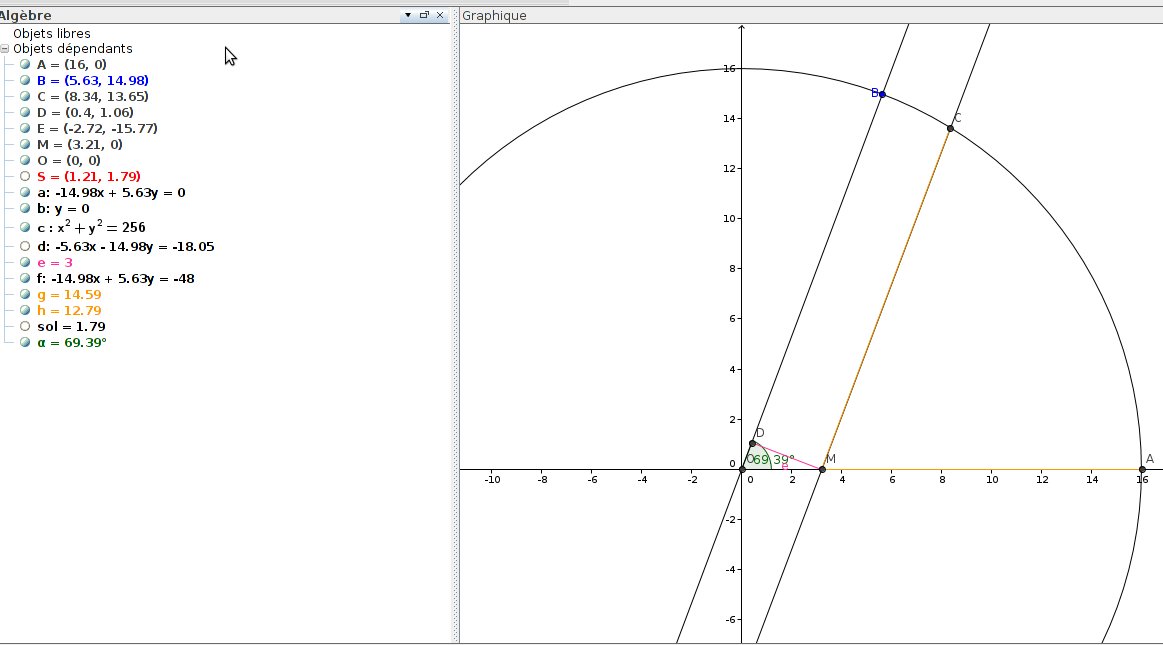
Soit \(D\) le projeté orthogonal de \(M\) sur la droite \((OB)\). On a par définition \(DM=e\). La trigonométrie nous donne \(\sin(\alpha)=\frac{DM}{OM}\) soit \(OM=\frac{e}{\sin(\alpha)}\). Il s’en suit que : \[MA=OA-OM=r-\frac{e}{\sin(\alpha)}\]
2. Calcul de la longueur MC
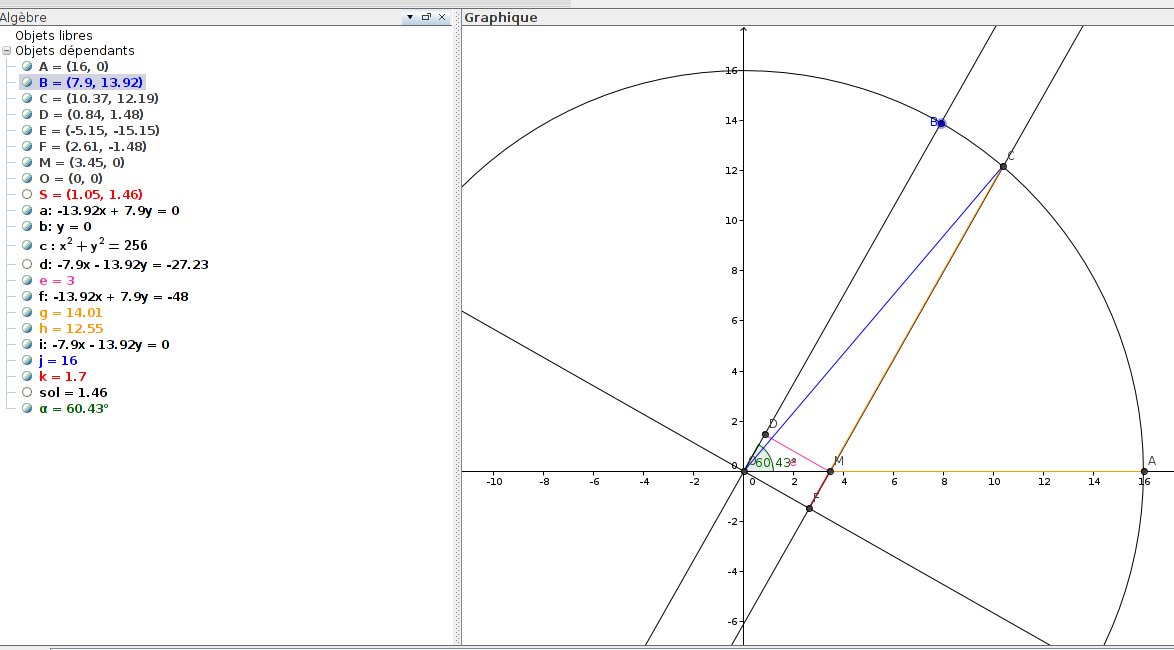
Soit maintenant \(F\) le projeté orthogonal de \(O\) sur \((MC)\). On a alors \(MC=FC-FM\). Par le théorème de Pythagore \(OC^2=OF^2+FC^2\) d’où \(FC=\sqrt{r^2-e^2}\). Ensuite \(FM=OD=\frac{e}{\tan(\alpha)}\), donc \[MC=\sqrt{r^2-e^2}-\frac{e}{\tan(\alpha)}\]
3. Etude de la fonction \(d(\alpha)=MC-MA\)
La fonction a étudier est la suivante : \[d(\alpha)=\left(\sqrt{r^2-e^2}-\frac{e}{\tan(\alpha)}\right)-\left(r-\frac{e}{\sin(\alpha)}\right)\]
ou écrit autrement : \[d(\alpha)=e\left(\frac{1-\cos(\alpha)}{\sin(\alpha)}\right)+(\sqrt{r^2-e^2}-r)\]
On remarque que l’étude s’effectue sur l’intervalle \([\alpha_{min},\alpha_{max}]\) où : \[\left\{\begin{array}{l}\alpha_{min}=\arcsin\left(\frac{e}{r}\right)\\\alpha_{max}=\pi-\arcsin\left(\frac{e}{r}\right)\end{array}\right.\]
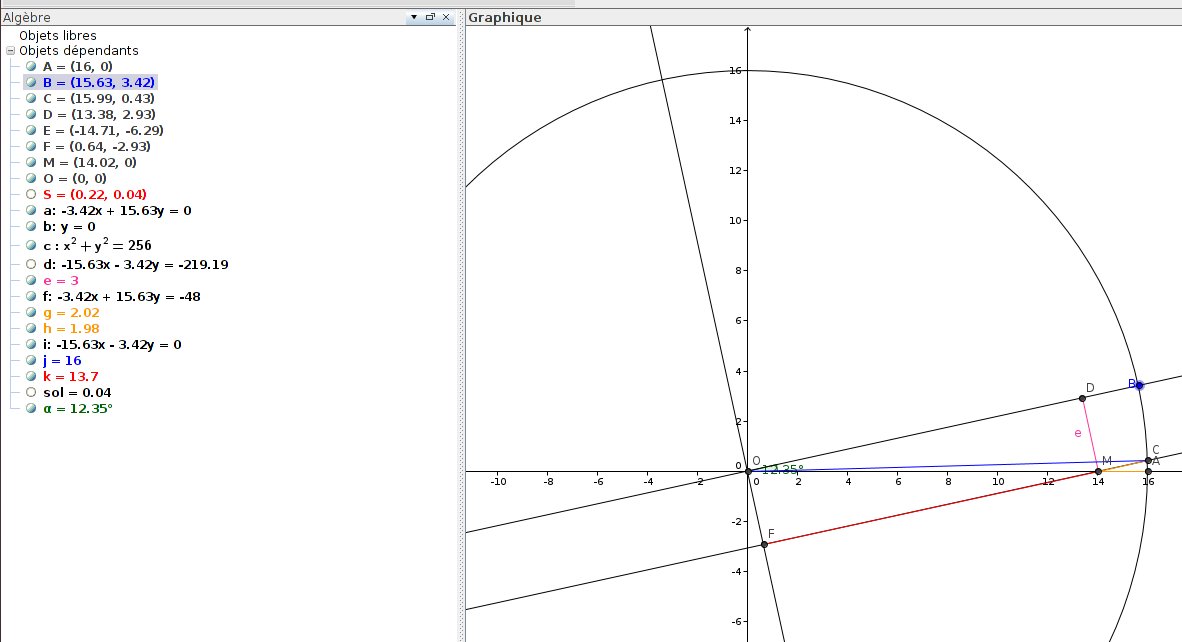
En effet quand \(B\) se rapproche de \(A\), l’angle limite pour lequel on conserve une distance \(DM=e\) est lorsque le point \(M\) est confondu avec \(A\), dans ces conditions \(\sin(\alpha_{min})=\frac{AD}{OA}=\frac{e}{r}\). On a la même chose symétriquement pour \(\alpha_{max}\).
On dérive la fonction et on obtient : \[d'(\alpha)=e\frac{\sin(\alpha)^2-(1-\cos(\alpha))\cos(\alpha)}{\sin(\alpha)^2}=e\frac{1-\cos(\alpha)}{\sin(\alpha)^2}=\frac{e}{1+\cos(\alpha)}\]
Comme \(\cos(\alpha)\) est compris entre \(-1\) et \(1\) alors \(d'(\alpha)>0\) sur l’intervalle \([\alpha_{min},\alpha_{max}]\) et ainsi la fonction \(d\) est continue strictement croissante sur cet intervalle. \(d\) est une bijection de \([\alpha_{min},\alpha_{max}]\) dans \([d(\alpha_{min}),d(\alpha_{max})]=[0,2\sqrt{r^2-e^2}]\).
On constate alors, en vertu de la croissance et du fait que \(d(\alpha_{min})=0\), que \(d(\alpha)\) reste toujours positive sur l’intervalle \([d(\alpha_{min}),d(\alpha_{max})]\) c’est-à-dire que le côté \(MC\) est toujours supérieur au côté \(MA\). On remarque également que le point \(M\), initialement confondu avec \(A\), décroît sur l’axe des abscisses jusqu’à la position d’abscisse \(r-e\) atteinte pour \(\alpha=\frac{\pi}{2}\), puis croît de nouveau pour atteindre le point \(A\) lorsque \(\alpha=\alpha_{max}\).
4. Inversion de l’équation \(d(\alpha)=C\)
On sait d’après ce qui précède que si \(C\in [0,2\sqrt{r^2-e^2}]\) alors l’équation \(d(\alpha)\) admet une unique solution \(\alpha_C\). Nous allons maintenant expliciter cette solution en reprenant l’expression initiale de \(d(\alpha)\).
En posant \(t=tan\left(\frac{\alpha}{2}\right)\) on a \(\sin(\alpha)=\frac{2t}{1+t^2}\) et \(\tan(\alpha)=\frac{2t}{1-t^2}\) d’où : \[d(\alpha)=\left(\sqrt{r^2-e^2}-\frac{e(1-t^2)}{2t}\right)-\left(r-\frac{e(1+t^2)}{2t}\right)=et+\sqrt{r^2-e^2}-r\]
Par conséquent on a : \[d(\alpha)=C\Leftrightarrow et+\sqrt{r^2-e^2}-r=C\Leftrightarrow t=\frac{C+r-\sqrt{r^2-e^2}}{e}\]
Finalement on en conclut que : \[\color{green}{\alpha_C=2\arctan\left[\frac{C+r-\sqrt{r^2-e^2}}{e}\right]}\]
Applications numériques :
Ma pizza a un rayon \(r\) de 16 cm, je coupe une “bande” d’épaisseur \(e\) de 3 cm. Je mesure la différence de longueur \(C\) entre les côtés \(MC\) et \(MA\) qui est de 2 cm. On trouve alors un angle initial \(\color{green}{\alpha_C\approx 74,56^{\circ}}\). On peut le vérifier sur la simulation geogebra (l’utilisateur faisant varier le point \(B\) sur le cercle).